Ахиллес и черепаха

user warning: Error writing file '/tmp/MYqg6Nj1' (Errcode: 28) query: SELECT c.cid as cid, c.pid, c.nid, c.subject, c.comment, c.format, c.timestamp, c.name, c.mail, c.homepage, u.uid, u.name AS registered_name, u.signature, u.signature_format, u.picture, u.data, c.thread, c.status FROM gadaika_comments c INNER JOIN gadaika_users u ON c.uid = u.uid WHERE c.nid = 607 AND c.status = 0 ORDER BY SUBSTRING(c.thread, 1, (LENGTH(c.thread) - 1)) LIMIT 2260, 10 in /var/www/drupal/modules/comment/comment.module on line 991.

Этот парадокс - одна из апорий (затруднений) Зенона. Автором этого парадоксального рассуждения является Зенон Элейский, древнегреческий философ, живший около двух с половиной тысяч лет назад (!).

Ахиллес и черепаха движутся по прямой в одну и ту же сторону, черепаха находится на расстоянии 1000 метров впереди Ахиллеса. Ахиллес бежит в 10 раз быстрее, чем ползёт черепаха.

Ахиллес никогда не догонит черепаху, ведь пока он пробежит 1000 метров до того места, где находилась черепаха, та уже отползёт на 100 метров вперёд. Когда же Ахиллес пробежит и эти 100 метров, черепаха отползёт ещё немного дальше. Это будет продолжаться бесконечно: каждый раз, когда Ахиллес бежит до места, где была черепаха, она уже отползёт на некоторое расстояние.

Сможете ли вы опровергнуть это утверждение?

Средняя оценка: 3.7 (94 голосов)
Темы:
Автор: gadaika, Чт, 03/25/2010 - 03:00

Познавательно

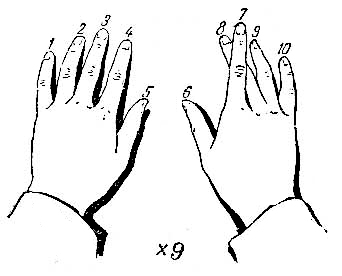Человеческая рука есть одна из первых счетных машин!

Движением пальца. Положите обе руки рядом на стол и протяните пальцы. Каждый палец слева направо будет означать соответствующее порядковое число: первый слева — 1, второй — 2, третий — 3, четвертый — 4 и т. д. до десятого, который будет обозначать число 10. Например, Нам необходимо умножить 7 на 9. Теперь поднимите седьмой палец. Число пальцев, лежащих налево от поднятого пальца, будет числом десятков произведения, а число пальцев направо — числом единиц. Налево от поднятого пальца лежат 6 пальцев, а направо — 3. Значит, результат умножения 7 на 9 равен 63.

Это удивительное на первый взгляд механическое умножение тотчас же станет понятным, если вспомнить, что сумма цифр в каждом произведении чисел таблицы умножения на девять равна девяти, а число десятков в произведении всегда на 1 меньше того числа, которое мы умножаем на 9. Поднятием соответствующего пальца это мы и отмечаем, а следовательно, и умножаем.

другие факты »